CS61B-Spring2024 学习记录

Java 基础

课程一共有 40 讲，其中前 12 讲主要是介绍一些 Java 基础相关的知识点。首先就是一些语言特性，这个都大差不差吧。通过对单链表和多链表的实现，基本上能引导一个有面向对象编程基础的同学入门 Java 语言。然后还介绍了数组和单元测试，因为我做的是 Spring24 版本的，只能在本地测试代码，而有些实验本地测试需要自己进行编写，不过好在现在有了 AI 的帮助，编写测试也变得比较简单了。

继承：接口和实现 Interface and Inplementation

• 重载：函数方法名称一样，仅仅是参数类型不同。
  • 缺点：超级重复和丑陋，需要维护多份基本一样的代码。

我们有 SLList、DLList 和 AList 等多种 List 的实现，这构成了一组 is-a 关系的层次结构。我们可以形式化这种关系，得到一个 superclass 超类 List，而具体的实现都称为它的子类。

而 List 就是 Java 所说的接口 Interface，指定了列表能够执行的操作，但并不提供实现。在具体的 AList 中，public class AList<Item> implements List61B<Item>{...}表明将会实现接口指定的属性和行为。

重写：Override，子类中实现超类指定的方法签名。

超类中可以使用 default 关键字提供某些方法的默认实现。

• 动态类型 dynamic type：比方说，一个 List 既是一个 List，也可能是一个 AList 实现，因此如果 List 提供了默认实现，而 AList 中又重写了该实现，会在其动态类型中搜索适当的方法签名并运行它。
• 重载没有上述特性，静态类型是什么就会执行静态的类型对于的方法。

继承：拓展、转换和高阶函数 Extends、Casting and HoF

Extends 扩展

一个类成为另一个类（不是接口）的下位词，就可以使用拓展。比如说我要在 AList 类的基础上，添加一些新的功能，得到 exAList，那么就可以使用public class exAList<A> extends AList<A>{...}拓展它。

不能继承构造函数，如果父类是无参数构造函数，而子类的构造函数中有参数，那么我们需要在子类的构造函数中显式调用 super() 函数来执行父类的构造函数。

Java 中每个类都是 Object 类的后代，都隐式的扩展了 Object 类。

Casting 转换

Static vs. Dynamic Type：Java 中的每个变量都有静态类型，这是声明变量时指定的类型，并在编译时检查。每个变量也有一个动态类型，该类型在变量实例化时指定，并在运行时检查。

而 cast 就是一种指定表达式编译时类型的方法，比如说我有一个 Dog 类，我可以将起赋值给 Animal 类，但是，我不能将 Animal 类赋值给 Dog 类，为了做到这一点，需要用到 cast，如下所示。使用 instanceof 运算符来确保实际类型是 Dog，然后进行转换。否则，编译时通过了检查，运行时可能出错。

Animal animal = new Dog(); // Upcasting
if (animal instanceof Dog) {
    Dog dog = (Dog) animal; // Downcasting
}

HoF 高阶函数

现在，Java 中有了函数式接口和 lambda 表示式，可以将函数作为参数。之前，需要使用下面的方法来实现：

public interface IntUnaryFunction {
	int apply(int x);
}

public class TenX implements IntUnaryFunction {
	public int apply(int x) {
   		return 10 * x;
	}
}

public class HoFDemo {
	public static int do_twice(IntUnaryFunction f, int x) {
   		return f.apply(f.apply(x));
	}
	
	public static void main(String[] args) {
   		System.out.println(do_twice(new TenX(), 2));
	}
}

继承：亚型多态性、比较器、可比性

Subtype Polymorphism 多态性

多态也就是多种形态，在 Java 中，多态指的是对象可以具有多种形式或类型，即一个对象可以被视为自己的类的实例、父类的实例、父类的父类的实例等等。

显式 HoF 方法：提供一种适用于该对象的比较方法、toString 方法。

def print_larger(x, y, compare, stringify):
    if compare(x, y):
        return stringify(x)
    return stringify(y)

亚型多态性（Subtype Polymorphism）方法，对象本身做出选择，取决与运行时类型。

def print_larger(x, y):
    if x.largerThan(y):
        return x.str()
    return y.str()

Comparables 比较

我们要为我们的对象实现 max() 函数，那么也就是说，需要能够比较两个对象。作为一个通用的最大值函数，它接受 Object 类型的参数（所有的类都是 Object 类的子类）。在比较时，不能使用 > 符号，因为该运算符并不适用于任意对象类型。

我们可以创建一个接口(Interface)，保证它的任何实现(implements)类（例如 Dog）都包含比较方法，我们将其称为 compareTo。Java 中已经为我们提供了这个接口，称为 comparable，要求实现类都实现 compareTo 方法。

public class Dog implements Comparable<Dog> {
    private String name;
    private int age;
    @Override
    public int compareTo(Dog other) {
        return this.age - other.age;
    }
}

比较器

comparable 接口为每个狗提供和与另一只狗进行比较的能力。但是，如果我想按照名字进行排序，又该怎么办呢？

Java 使用 Comparator 来解决该问题。比较器是一个对象，也是一个接口，要求任何实现类都实现 compare 方法，规则和 compareTo 类似。我们可以把实现类嵌套在 Dog 类里面，也可以将其在外部实现（不需要修改原始类就能对其排序）。

public class AgeComparator implements Comparator<Dog> {
    @Override
    public int compare(Dog p1, Dog p2) {
        return p1.getAge() - p2.getAge();
    }
}

List<Dog> dog = // ...
Collections.sort(dog, new AgeComparator());

1. Comparable 提供单一的排序标准，Comparator 可以提供多种排序标准。
2. Comparable 修改类本身，Comparator 不需要修改比较的类。
3. Comparable 接口方法是 compareTo，Comparator 接口方法是 compare。
4. Comparable 通常略微更高效，因为比较逻辑直接在对象中。
5. Comparator 需要额外的对象，但提供了更大的灵活性。

继承：迭代器和对象方法 Iterators and Object Methods

迭代器

只有实现了迭代器，才能使用增强型的 For 循环，即 for(String word : words)。

和比较器一样，我们要的是一个迭代器对象，这个对象需要实现 hasNext() 和 next() 两个方法。但是，有一点点区别，集合(Collection)类已经实现了 Iterable 接口，这要求对象重写 iterator() 方法，该方法返回一个 Iterator 对象。

而一个 Iterator 对象需要实现 Iterator 接口，这要求对象重写 hasNext() 和 next() 两个方法。

public class MyList<T> implements Iterable<T> {
    ...
    @Override
    public Iterator<T> iterator() {
        return new myIterator();
    }
    public class MyIterator<T> implements Iterator<T> {
        ...
        @Override
        public boolean hasNext() {}
        @Override
        public T next() {}
	}
}

• 仅仅实现 Iterator 类不能使用 foreach 循环，而实现了 Iterable 类的可以。
• Iterable 是可以被迭代的对象，Iterator 是执行迭代的对象。

对象方法 Object Mathods

所有类都继承自总体 Object 类，也都会继承 toString()、equals()、hashCode() 等方法。我们可以继承来重写这些方法，以按照我们希望的方式运行。

不相交集

• 使用根节点对应 parent 数组值的绝对值代表树的权重，用于 Quick Union。
• 在 Find 时执行路径压缩，将路径上的节点全部都挂到根节点上。可以使用栈+迭代或者递归来解决。

BST、B-Tree and LLRBs

二叉搜索树：更优雅的查找、插入和删除。

static BST find(BST T, Key sk) {
    if (T == null)			return null;
    if (sk.equals(T.key))	return T;
    else if (sk < T.key)	return find(T.left, sk);
    else					return find(T.right, sk);
}
static BST insert(BST T, Key ik) {
    if (T == null)			return new BST(ik);
    if (ik < T.key)			T.left = insert(T.left, ik);
    else if (ik > T.key)	T.right = insert(T.right, ik);
    return T;
}
static BST delete(BST T, Key dk) {
    if (T == null) 			return null;
    if (dk < T.key) 		T.left = delete(T.left, dk);
    else if (dk > T.key)	T.right = delete(T.right, dk);
    else {
        if (T.left == null) return T.right;
        if (T.right == null) return T.left;
        BST successor = findMin(T.right);
        T.key = successor.key;
        T.right = delete(T.right, successor.key);
    }
    return T;
}

B 树：自平衡树，每个节点的高度都一样，但是实现较为复杂。

每个节点最多包含 3 个项目的 B 树称为 2-3-4 树。每个节点最多 2 个项目的 B 树称为为 2-3 树。前者用来实现标准红黑树，后者可以用来实现左倾红黑树。

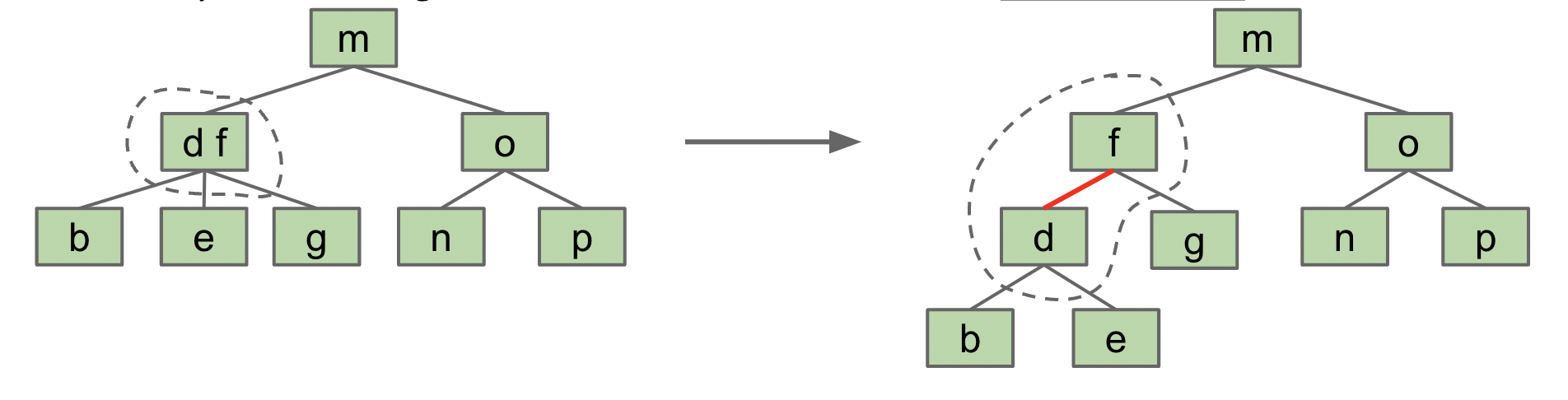
LLRB 左倾红黑树：通过 2-3 树得到的，如下，我们需要把 d 设为红节点，f 设为黑节点。因此，根节点是黑色的、红节点不相邻、从根节点到任意一个叶节点经过的黑节点数量相同。

插入也比较简单，进行一些旋转和颜色翻转操作即可。

哈希、堆和优先队列

只有不可变(Immutable)类型是可哈希的。

Hash Code

并不是所有的对象都能转换为数字，因此，需要通过哈希算法将对象转换为数字表示，并且数字是尽可能随机的。但是这样内存效率太低下了，故使用模运算将其映射到小范围数字上。

在 Java 中， Math.floorMod 函数将在正确考虑负整数的同时执行模运算，而 % 则不会。

碰撞避免

1. 线性探测：将冲突键存储在数组中的其他位置，如下一个开放数组空间。
2. 拉链法：将具有相同哈希值的所有键一起存储在集合中，如 LinkedList 。这种共享单个索引的条目集合称为存储桶。

通过负载因子调整数组的长度。

优先队列

优先队列是一种抽象数据类型，可优化处理最小或最大元素。
使用这种专门的数据结构可以带来空间/内存方面的好处。

堆

1. 原地建堆：从最后一个元素判断到第一个元素，如果有反序，则交换。
2. 空出第一个元素不存储数据，这样parent(k) = k / 2，处理逻辑更简单。

图

图的表示和遍历

图可以使用邻接表或者邻接矩阵来进行存储。

public class Graph {
  public Graph(int V):               // Create empty graph with v vertices
  public void addEdge(int v, int w): // add an edge v-w
  Iterable<Integer> adj(int v):      // vertices adjacent to v
  int V():                           // number of vertices
  int E():                           // number of edges
...

1. 树的层序、前序、中序和后序遍历。
2. 图的广度优先遍历（对应于层序遍历），前序深度优先遍历和后序深度优先遍历。

在使用 BFS 时，我们维护一个 edgeTo 数组，其中 edgeTo[n] = v 表示到达节点 n 的前一个节点是节点 v；再维护一个 distTo 数组，其中 distTo[n] = distTo[v] + 1，表达到达节点 n 的距离。

最短路径算法

当图的边没有权重时，可以使用 BFS 算法查找最短路径。如果有权重，也可以使用 BFS 算法，只不过不使用 mark 数组来对节点进行访问标记，而是通过判断是否能减小 distTo 数组的大小，如果能，则该节点需要进入队列并更新其值。

迪杰斯特拉算法

Dijkstra 算法接收输入顶点 s，并输出从 s 开始的最短路径树，能够处理非负有权图。

1. 创建优先队列。
2. 将 s 添加到优先队列中，优先级为 0，而其他所有顶点优先级为 ∞。
3. 当优先队列不为空时，弹出一个顶点，并 relax 从该顶点出去的所有的边。
4. 计算潜在距离、检查是否得到更好优先级以及潜在更新的整个过程称为 lelax。

def dijkstras(source):
    PQ.add(source, 0)
    For all other vertices, v, PQ.add(v, infinity)
    while PQ is not empty:
        p = PQ.removeSmallest()
        relax(all edges from p)
def relax(edge p,q):
   if q is visited (i.e., q is not in PQ):
       return
   if distTo[p] + weight(edge) < distTo[q]:
       distTo[q] = distTo[p] + w
       edgeTo[q] = p
       PQ.changePriority(q, distTo[q])

A* 算法

假设我希望得到从 A 到 B 的最短距离，我根本不用构建一棵从 A 开始的最短路径树，这太昂贵了。

A* 又叫启发式搜索，在迪杰斯特拉算法的基础上，如果一个搜索的方向在直线距离上远离了目标节点，那么我们就施加一个惩罚值降低它在优先队列中的优先级，而如果物理上靠近，我们可以给个奖励值。这样得到的结果虽然不能保证是最优解，但是可以大大的加快速度。

而惩罚和奖励则取决于我们的启发方法。

最小生成树 MST

Prim 算法（加点法）

1. 从一个节点开始。
2. 添加有一个节点在 MST 中的最短边。
3. 重复此操作，直到 MST 中出现 V -1 条边。

本质上，该算法通过与 Dijkstra 算法相同的机制运行。唯一的区别是，Dijkstra 根据候选节点与源节点的距离来考虑候选节点，而 Prim 则着眼于每个候选节点与正在构建的 MST 的距离。

Kruskal 算法（加点法）

1. 将所有边从小到大排序。
2. 一次取一条最小权重的边（边两端的节点没有已连接），将其添加到 MST 中。
3. 重复此操作，直到 MST 中出现 V -1 条边。

由此我们看出，克鲁斯卡尔算法需要使用并查集作为辅助用于判断顶点是否联通；使用优先队列对边进行排序。

拓扑排序和 DAG

DAG 是有向无环图。

拓扑排序

方法一：需要记录一个入度 inDegree 数组，采用类似 BFS 的遍历算法。如果存在环路，那么将会有顶点一直不能入队，结果列表不满。

方法二：依次对图中每个顶点依次（随意顺序）执行 DFS 遍历，将后序遍历结果写入后序排列列表中，最后将列表反转即可。这种做法只适用于有向无环图，如果有环，则无法判断。我们可以使用一个 onStack 数组来在 DFS 时检测是否存在环路。

DAG 上的最短路径

存在负边时，迪杰斯特拉算法失效，但是我们可以按照拓扑顺序访问顶点，每次访问时，relax 所有的向外的边。

前缀树

非常适合存储字符串，对于前缀匹配效果很好，比如说搜索引擎的搜索提示就是前缀匹配。

public class TrieSet {
   private static final int R = 128; // ASCII
   private Node root;    		// root of trie

   private static class Node {
      private char ch;  
      private boolean isKey;   // 是否为结束字符
      private DataIndexedCharMap next;

      private Node(char c, boolean blue, int R) {
         ch = c; 
         isKey = blue;
         next = new DataIndexedCharMap<Node>(R);
      }
   }
}

排序

选择排序

堆排序

归并排序

递归，排序时间很稳定。但不太能利用局部性原理，慢于快速排序。

插入排序

十分适用于元素数量较少时和数据基本有序时，衍生出希尔排序。

快速排序

最坏情况下，退化到 O(n^2)，在已经排好序的情况下。

优化策略：

1. Pivot Selection：随机选择、选最左边、选三个取中位数等。
2. Randomization：随机化，在排序前稍微进行一下洗牌 shuffle，避免最坏情况。
3. Three-way Partitioning：三项切分，大于小于和等于，适用于有大量重复元素的情况。
4. Hybrid Sorting：混合排序，长度较小时改用插入排序。

利用归并排序或者快速排序的原理，可以将查找中位数的时间复杂度缩减到 O(n)。

基数排序

LSD 最低有效数字基数排序

MSD 最高有效数字基数排序

适用于数量巨大的数字or字符串排序，如排序 QQ 号。

每次字符串不是只能处理一位，其实可以分多个块，如分 256 个块，对于数字也就是一次处理 8 个 bit。

压缩和复杂性

压缩模型：在比特上应用算法

摩尔斯电码

使用的是字母到符号的 Map。相同的符号序列可以表示不同的字母序列，因此，需要在码字之间添加暂停表示中断。

无前缀编码

在无前缀代码中，没有代码字是任何其他代码字的前缀。这样，可以避免摩尔斯电码的混淆问题。

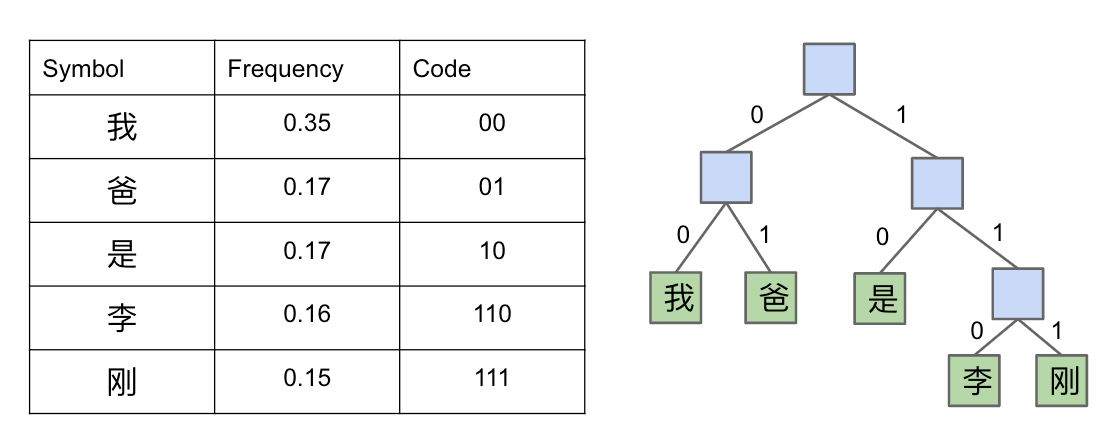
香农-法诺码 Shannon-Fano Codes

Shannon-Fano 码是一种基于一组符号/字符及其概率创建无前缀代码的方法。主要思想是，我们希望为更受欢迎的字符提供更短的无前缀代码，为较少使用的字符提供更长的代码。

• 计算文本中所有字符的相对频率。
• 按照频率分为大致相等的左右两个部分。
• 左半部分有一个前导 0，右边部分有一个前导 1。
• 在左右子树上重复该过程。
  

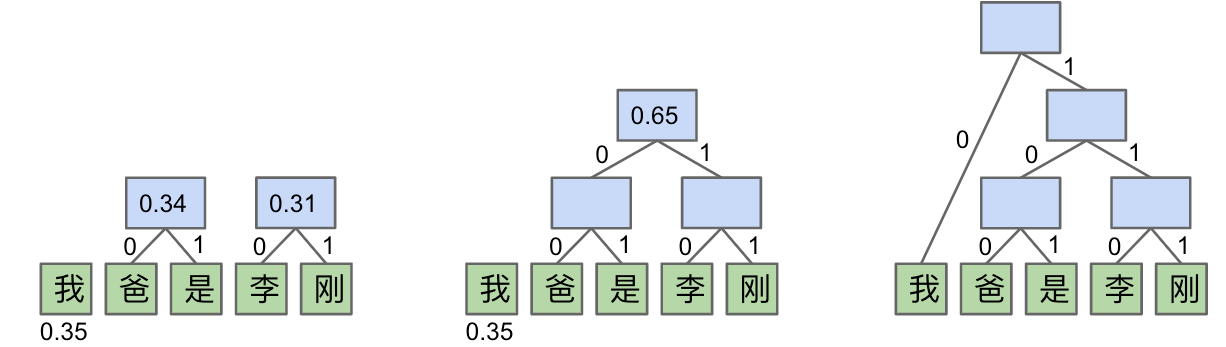
霍夫曼编码 Huffman Coding

霍夫曼编码对无前缀码采用自下而上的方法，而不是香农-法诺码采用自上而下的方法。

• 计算相对频率，每个符号作为一个节点，权重为相对频率。
• 取权重最小的两个节点将他们合并为一个大的节点，权重为小节点权重之和。
• 重复第二步，直到节点池中只剩下一个节点。即得到了一棵霍夫曼树。
  

压缩比

数据压缩的目标是减小数据序列的大小，同时保留尽可能多的信息。例如，字母 e 在英语词典中出现的频率比 z 更高，因此我们希望用更小的位来表示 e 。

• 压缩比：是压缩数据的大小与原始数据的差异程度的度量。
• 霍夫曼编码：用更少的位数表示常见符号，从而实现更高效的编码。
• 游程编码Run-length encoding：用字符本身及其出现的次数来替换重复的字符。
• LZW：搜索输入中常见的重复模式并用较短的代码替换它们。

压缩模型：自提取位

输出不仅包括压缩比特流，还包括用于解压缩的算法。

例如：我们将图片按 8 位分块之后，进行霍夫曼编码后把文件给别人，别人可能不知道如何解压缩它。因此，我们还需要提供霍夫曼编码的解码算法，可以单独进行发送。但是，在当前压缩模型下，更好的做法是将压缩的比特流打包到解码器的 byte[] 数组中。当文件传递给解释器时，该比特流就会直接生成原始数据。

LZW 压缩

• 初始化字典：对于 ASCII 文本，每个字符分别对应其 ASCII 码。
• 压缩过程：
• 读取输入数据的第一个字符，将其作为当前字符串。
  • 读取下一个字符 K。如果 W+K 在字典中，则当前字符串 W = W + K；
  • 否则，输出 W 在字典中的索引，将 W + K 加入字典，设置 W = K。
  • 重复以上步骤，直到处理完成，最后输出 W 在字典中的索引。

可以仅从压缩比特流重建原始比特流，而不需要将算法与压缩数据一起发送。

Labs

Lab 1：Setup

这个实验就是一些 git 和骨架代码的使用说明。然后就是 IntelliJ （我跟喜欢叫它 IDEA）的安装说明。蛮有趣的一个部分是老师甚至还给出了它喜欢的配色方案，我就喜欢搞这些有的没得的，更容易入门。

其实用 Vscode 也可以，安装好 Java 和插件之后，把提供的库文件导入进去就可以了。不过试了一下，代码补全功能离 IDEA 还差得远。

Lab 2 and 3：Debugging

实验文档会一步一步的教我们如何使用 IDEA 的调试功能，同样也设置了几个简单的实验，就像 CSAPP 的 Bomb Lab 一样，让我们利用调试工具来拆弹。

Lab 4：git

使用一些 git 命令，找到 password，形式上和 CTF 有点像，总之也是比较简单的了。

Lab 5：Disjoint Sets

实现一个不相交集。在路径压缩部分，我们可以利用栈存储路径上的所有节点，最后将其挂到根节点上，也可以使用递归来解决。

在 Union 时，使用加权快速联合，根节点对应的 parent[i] 的值的绝对值表示树上的节点的个数。权重已经基本可以反应出树的高度了，因此没有使用按秩合并的方法。

Lab 6：BSTMap

使用二叉搜索树来实现一个 Map。

其中插入、查找和删除都能使用递归来解决，之前我写的递归一直不够优雅，这门课上教过之后受益匪浅，递归到最深的层次，代码写起来反而更简洁清楚。

实现二叉搜索树的迭代器需要使用到栈来存储已经遍历过的数据。首先，父类需要 extends Iterable<K>，然后 BSTMap 中需要实现 iterator() 方法，该方法返回一个类。这个类需要 implements Iterator<K>，也即需要实现 hasNext 和 next 两个方法。

我在实现的过程中，因为把 Iterable 写成了 Iterator，走了蛮多弯路。

Lab 7：LLRB

实现左倾红黑树，这里只要求实现插入方法。本来觉得红黑树实现起来很难，但是最后发现还是很简单的，左倾红黑树实现比标准红黑树简单的多，但是性能却差不多。

private RBTreeNode<T> insert(RBTreeNode<T> node, T item) {
    if (node == null) {
        return new RBTreeNode<>(false, item);
    }
    if (item.compareTo(node.item) < 0) {
        node.left = insert(node.left, item);
    } else if (item.compareTo(node.item) > 0) {
        node.right = insert(node.right, item);
    }
    if (isRed(node.right) && !isRed(node.left)) {
        node = rotateLeft(node);
    }
    if (isRed(node.left) && isRed(node.left.left)) {
        node = rotateRight(node);
    }
    if (isRed(node.left) && isRed(node.right)) {
        flipColors(node);
    }
    return node;
}

Lab 8：HashMap

我们的哈希表使用拉链法来避免冲突。插入时，找到对应的 bucket，如果 bucket 里面有这个 key，那么只是简单的替换 value 即可，如果没有这个 key，可以创建一个新的 Node 并将其插入。如果填充因子达到了上限，就进行扩容。

这里删除没有要求缩减容量，然后就是不能简单的用 hashcode() % capacity 来找到索引，而是要使用 floorMod 方法。

迭代器的实现我们可以使用 bucket[i] 内部的迭代器和变量 i，只有 i == capacity 时才遍历完成，只有 iterator.hasNext() == null 时才增加 i 的值。

Lab 9：Conway’s Life

这个实验是为 Project 3 做准备的，nextGeneration 按照说明来实现就行了，然后就是持久化部分，我们需要将 board 保持到文件中，然后在需要的时候从文件中提取出来。

saveBoard 要原本左下角为 (0, 0)，骨架代码中已经为我们实现了转置和翻转的代码，因此，我们只需要找到合适的遍历方向，将数据存储到文件中即可。

Lab 10：Tetris

这个实验也是为 Project 3 做准备的，实现了交互。updateBoard 方法、incrementScore 方法、 clearLines 方法、renderScore 方法按照说明来就好了。 clearLines 方法我们逐行判断是不是满了，然后从上到下，如果有一行满了，那么则将其上面的块全部都往下挪一块。（如果时从下到上判断，那么往下挪了一行之后，还得从当前行继续判断。

有一种效率更高的方法是先求好每一行需要下移的行数，比如下面消掉了两行，那么就记录为 2，这样可以减少移动的次数。

游戏的流程如下，生成一个新的块，如果游戏结束，那么退出。否则一直更新板并显示板，除非这个块消失了。然后我们清除多余的行，并显示板。

public void runGame() {
    resetActionTimer();
    while (true) {
        spawnPiece();
        if (isGameOver()) {
            System.out.println("Game over!");
            exit(0);
        }
        while (getCurrentTetromino() != null) {
            updateBoard();
            renderBoard();
        }
        clearLines(board);
        renderBoard();
    }
}

Homeworks

作业 1 3 4 是书面作业，非伯克利学生无法访问。

Homework 0

是一些 Java 语法和基础数据结构。

Homework 2

渗透，判断水是否能从最上面渗透到最下面，我们使用并查集来写。对于每个空，有三种状态，实心、空心和有水。当一个块从实心变成空心时，我们需要将其和四周的块进行 Union，如果四周块的根节点有水或者当前块为最上面一行的块，我们将 Union 之后的根节点设为有水。仅通过根节点来判断是否有水。

判断是否渗透，需要遍历最下面一行，如果有节点是有水的，那么就渗透，否则不渗透。

优化：我们设置一个虚拟头节点，通过判断是否和虚拟头节点相连来确定是否有水。在 open 时，仅进行 Union 操作，如果是顶行，那么和虚拟头节点进行 Union。这样每个节点只有两个状态，可以使用布尔值来表示，分别是开和关。

但是这种优化在判断是否渗透时不起作用，还是需要 O(n) 的时间复杂度。如果设置一个虚拟底节点，那么水就会通过虚拟底节点连同，使得 isFull 方法判断不准确。

如果非要优化 percolates 方法，那么我们可以用两个并查集，一个只有虚拟头节点，用来判断 isFull，另一个有虚拟头节点和虚拟底节点，如果这两个节点时 connected 的，那么就说明渗透了。这是一种用时间换空间的做法。

Projects

Project 0：2048

这个任务的文档很详细，基本上怎么做已经完全说清楚了。比较巧妙的一个地方在于，仅仅使用不同的视角，就能从处理一个方向拓展到处理四个方向。

做完这个项目，得到的结果就是一个能真正上手去玩的 2048 小游戏了，成就感满满的。

Project 1A：LinkedListDeque

我们可以使用带哨兵节点的双向链表来实现 Deque 数据结构。题目要求 get 方法需要使用递归来实现，那么我们只需要一个辅助函数即可。

Project 1B：ArrayDeque

使用数组来实现 Deque，在 Java 中需要使用 deque = (T[]) new Object[8] 来创建范型数组。在插入之前，需要先判断是否已经满了，如果已经填满则需要进行扩容；在删除之后，如果不足容量的 1/4，则需要缩减容量。

我们使用两个指针来指向 Deque 的头和尾，其中 first 指向队列头，last 指向队列尾的后一个元素。

Project 1C：Deque Enhancements

实现迭代器，注意父类是要 extends Iterable，子类需要返回一个 implements Iterator 的类。

• Iterable 是一个接口，定义了一个类可以被迭代的能力。实现 Iterable 接口的类需要提供一个 iterator() 方法，该方法返回一个 Iterator 对象。

• Iterator 是一个接口，定义了迭代器的行为。实现 Iterator 接口的类需要提供 hasNext()、next() 和可选的 remove() 方法。

• Iterable 接口的实现类可以专注于管理和存储元素，而不必关心具体的迭代逻辑。

• Iterator 接口的实现类可以专注于定义如何遍历元素。

实现 equals 和 toString 方法，这两个方法都是 Object 类就规定有的，但是不太符合我们的需求，因此，我们需要 Override 它。toString 没有参数，我们直接实现即可，只需返回一个字符串。

public boolean equals(Object other) {
    if (this == other) {
        return true;
    }
    // instanceof 安全地进行类型检查和类型转换
    if (other instanceof ArrayDeque61B<?> otherDeque) {
        if (this.size() != otherDeque.size()) {
            return false;
        }
        for (int i = 0; i < this.size(); i++) {
            // 字符串的话，需要使用 equals 来比较
            if (!this.get(i).equals(otherDeque.get(i))) {
                return false;
            }
        }
        return true;
    }
    return false;
}

实现 MaxArrayDeque，我们拓展 ArrayDeque 即可。

public class MaxArrayDeque61B<T> extends ArrayDeque61B<T> {
    private final Comparator<T> comparator;
    public MaxArrayDeque61B(Comparator<T> c) {
        super();
        comparator = c;
    }
    public T max() {
        if (isEmpty()) {
            return null;
        }
        T max = get(0);
        for (int i = 0; i < size(); i++) {
            if (comparator.compare(get(i), max) > 0) {
                max = get(i);
            }
        }
        return max;
    }
}

Guitar Hero

利用 Deque 很方便做，挺简单的。

Project 2A：NGrams

TimeSeries 是一个拓展了 TreeMap 的类，其中 key 是年份，而 value 是该年出现的次数。我们主要实现加法和除法两种运算。其中加法原则上是个求并集的运算。都有则相加，只有一个有则取一个。

其中设置了 MIN_YEAR 和 MAX_YEAR 两个静态变量，可以大幅减轻我们处理问题的难度。

在 NGramMap 中，我创建了两个变量，一个是 TimeSeries 类型，用于存储每一年有有多少个单词；另一个是 Map<String, TimeSeries> 类型，用于统计每个单词在每年出现的次数。

Project 2B：Wordnet

首先我们实现图类，利用给定的文件，建立一个图，节点使用数字表示。图里需要两个邻接表，一个正向一个方向，实现两个方法，一个方法是找出所有的后续节点包括自己，另一个方法是找出所有的前驱节点包括自己，使用 DFS 递归算法。

然后创建 wordNet 类，里面有如下三个主要变量：

Map<Integer, List<String>> id2words;
Map<String, List<Integer>> word2ids;
Graph graph;

一个 ID 可能有多个单词，一个单词也可以存在于多个 ID 中。

要找到一个单词所有的下位词，我们需要找到该单词对应的 ID，然后利用 ID 在图上执行算法，找到所有的后继 ID，再找到这些 ID 对应的单词。使用 TreeSet 来存储结果单词，这样就可以天然的做到有序以及去重。

Project 2C：Enhancements

对于 K 不等于 0 的情况，我们需要统计每个单词出现的次数，而不是频率，因此需要将该单词不同年数的次数进行求和，利用 data 方法得到 List，然后使用 Java 流进行求和规约。我们把和的相反数作为 key 存入 TreeMap，这样遍历 TreeMap 得到的就是按出现次数排序的单词列表了。然后我们将单词写入 TreeSet 返回，也就实现了单词按照顺序排列。

private Set<String> helper(Set<String> words) {
    if (k == 0) {
        return words;
    }
    Map<Double, String> count = new TreeMap<>();
    Set<String> result = new TreeSet<>();
    for (String word : words) {
        List<Double> value = ngm.countHistory(word, startYear, endYear).data();
        if (!value.isEmpty()) {
            count.put(-value.stream().reduce(0.0, Double::sum), word);
        }
    }
    for (String word : count.values()) {
        if (k > 0) {
            result.add(word);
        }
        k--;
    }
    return result;
}

当然也可以使用优先队列进行排序，但是感觉 TreeMap 和 TreeSet 用于去重和排序真的蛮方便的。

共同祖先也就是上位词和下位词基本一样，就不赘述了，因为建图的时候我们也建了逆序图，所以处理起来很简单。

Project 3C：BYOW

利用的就是 Lab 9 和 Lab 10 中提供的代码和方法，建立一个二维的地图，然后进行一些操作。这种开放性的问题其实更像是软件工程问题，有四节 Lecture 都是讲软件工程，但是我对这个不是很感兴趣，而且我也没有 Autograder，就没做了。

TODO

gitlet 实验